铁打的DeltaS=0.02，流水的HFSS版本。碎片三分钟逛电巢App，收获一丢丢。

　　岛主用到的HFSS最老版本是6.0，运行在Unix系统中，看起来是昂贵的高大上Sun工作站，也许10万人民币一台，但却是命令行式的建模操作。

　　从HFSS8.0开始，慢慢转到Windows系统，图形化界面，菜单式建模操作，当年的硬件条件：单核奔腾CPU主频大概在300MHz，运行内存1G，普通电脑大概1万人民币一台。

　　为了适配当时的硬件环境，兼顾仿真速度和仿真精度，HFSS缺省设置DeltaS=0.02。或者说 ΔS = 0.02。

　　摩尔定律，星转斗移。同样的价格，估计现在的主频升到原来的10倍，CPU到64核心，运行内存提升了100倍以上，HFSS经历了十几次版本升级，但DeltaS缺省值仍然是0.02。

　　关于Passes、DeltaS、仿真精度、收敛

　　可以用一幅图形象地描述这几个概念的关系，一看就懂：

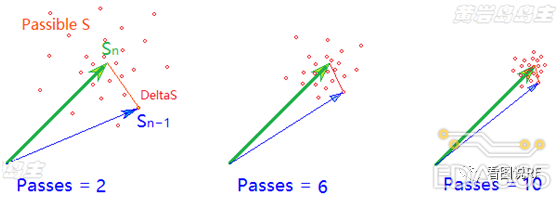
　　S参数有幅度和相位，用欧拉公式可转化为复平面上的实部和虚部，上面是用复平面内表示S参数矢量的，DeltaS自然也是矢量。

　　绿色粗箭头表示第n次剖分求解得到的某个S参数;

　　蓝色细箭头表示某个具体的模型第n-1次剖分求解得到的同一个S参数;

　　每一个红点都表示不同的模型在第n-1次剖分求解得到的可能的S参数(Passible S);

　　红色细线就表示矢量减法计算出来的DeltaS;

　　随着仿真次数Passes的增加，网格剖分越来越细，仿真精度越来越高，Sn越来越与真实的S参数接近，于是DeltaS模值也越来越小，也就意味着S参数越来越收敛。

　　Delta S定义

　　Delta S本质上是第n-1次求解得到的S参数与第n次求解得到的S参数之矢量差的模值的最大值。非常拗口。

　　公式如下：max|ΔS| = max|Sn-1-Sn|

　　绝对值符号表示模值，定义成一个矢量在复平面(或极坐标平面)上到圆点的距离。

　　下图表示设置不同的ΔS，求解得到的S参数与可能的S参数之间的关系。

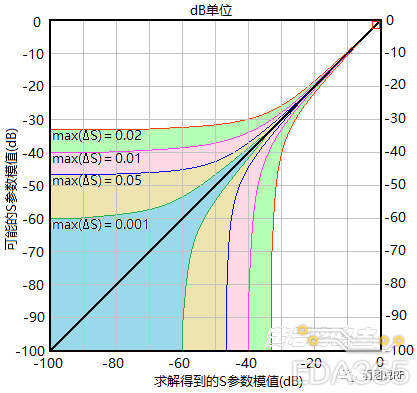
　　将上图右上方的红色小方框放大，并且用S参数(电压响应)模值(线性)展开成下图：

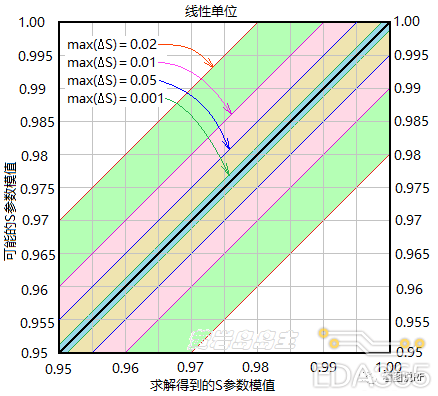
　　天线振子只有一个端口，所以只看S11的ΔS，无所谓ΔS最大值max。如果是两端口的传输线，则有4个S参数，那就找这4个S参数中的ΔS最大值max。

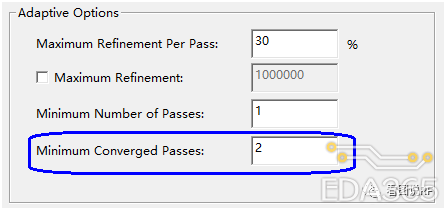
　　所以单端口模型的仿真有较大的几率出现“假收敛”，因此在HFSS中要设置最小收敛次数为2或3或4，看情况而定：

　　ΔS对仿真精度影响的真实案例

　　下图是一个网格地平面的微带线阻抗TDR仿真，随着DeltaS的不同，则阻抗有1.5欧的差异。

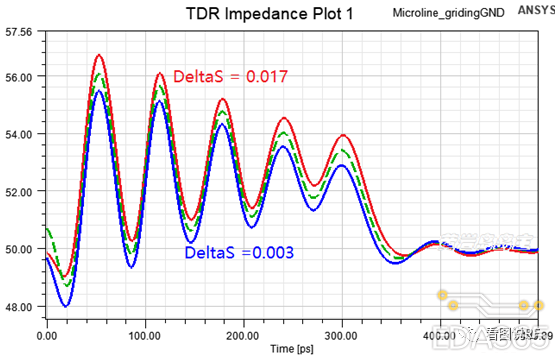
　　下图是某模型仿真Waveport端口阻抗的情况，可见DeltaS的不同，端口阻抗有较大的误差：

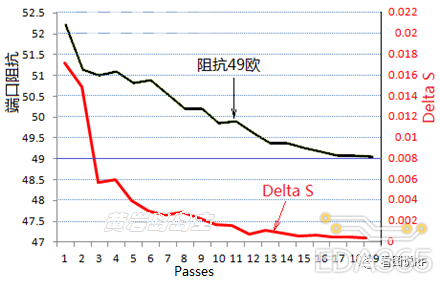
　　DeltaS=0.02，则端口阻抗误差达到6%。

　　下图是匹配良好的理想微带线的回波损耗S11与ΔS的关系：

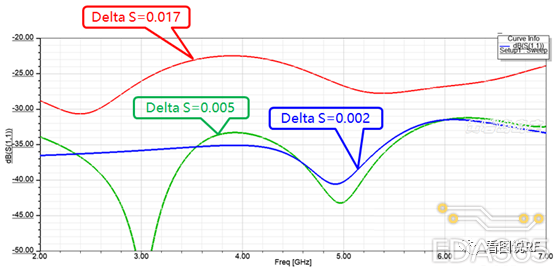
　　红色线DeltaS =0.017，仿真得到的S11=22dB，匹配良好的理想微带线来说，精度是不够的。

　　匹配良好的理想微带线，S11至少要优于30dB吧。

　　前几篇文章反复提过：25dB定向性指标的微带双线耦合器，各端口S11测试值至少要优于30dB，才不会影响测试精度。

　　总结

　　可见铁打的DeltaS = 0.02，这个缺省设置有问题。

　　ΔS = 0.02一般用于模型前期优化阶段的粗略仿真，效率优先;

　　ΔS = 0.005甚至0.002，用于后期定型投板的精细仿真，精度优先;

　　对于数量较少的端口，要在HFSS中设置最小收敛次数为2或3或4;